在以往资料分析的学习中，除了部分杂糅类的题目，最复杂的计算就是关于基期三兄弟的计算，即基期比重、基期倍数、基期平均数。这几个名词虽然概念上略有差别但由于本质上都是比例(除法)关系，且求的都是基期量，所以对应的公式都可以用一种式子去表示，因此计算方法上也是一模一样的。

　　首先回顾一下基期三兄弟的公式：。A指的是公式分子的现期量，B指的是公式分母的现期量。a指的是分子的增长率，b指的是分母的增长率。

　　由于公式中既有量的比值关系，又有(1+增长率)的比值关系，且还要将他们相乘，所以一旦选项比较接近时，按照常规的计算方式花费时间很长，计算时还容易出现错误。所以华图教育给大家介绍两种基期比重的计算方法，帮助大家快速秒杀选项。

　　1. 算一半

　　通过观察公式，进一步发现左边A/B其实就是两个量现期的比(即现期比重、现期平均数、现期倍数)。所以可以先算出A/B，并且算出的这一部分大概率还会出现在四个选项中，作为干扰选项出现，这也为我们判断出正确选项提供了方便条件。算出这一半后，我们可以去寻找另一半与1的大小关系：，则。从而根据选项判断出正确答案，简化了计算步骤。

　　【例1】2017年上半年，全国居民人均可支配收入12932元，比上年同期名义增长8.8%。全国居民人均工资性收入7435元，增长8.6%，占全国居民人均可支配收入的比重为57.5%;

　　2016年上半年，全国居民人均工资性收入占全国居民人均可支配收入的比重约为：

　　A. 53.6%

　　B. 57.6%

　　C. 60.6%

　　D. 63.6%

　　【答案】B

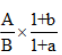
　　【解析】根据基期比重=，代入公式得，左边这一半由于题目中已经给出，无需计算，右边一半由于8.8%略大于8.6%，应略大于1，故最后结果应略大于57.5%，B选项最接近。

　　正确答案为B选项。

　　当然以上这种题目属于增长率a、b较接近，且通过分析就能得出答案，而考试中也会碰到不这么“凑巧”的题目。这就需要我们掌握第二种方法。

　　2. 拆1法

　　拆1法，顾名思义，即拆出来1进行简化计算，所以先将基期公式做进一步推导。

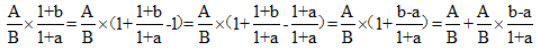
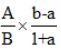
　　当选项较为接近，且算一半判断不出正确答案时，拆1法可以帮助我们判断基期值比算出的一半(现期值)具体多了。由于a、b均为百分数，所以相减再除以(1+a)远比计算容易的多。

　　以一道真题为例。

　　【例2】2018年我国全年境内外专利申请432.3万件，比上年增长16.9%;授予专利权244.7万件，增长33.3%。

　　2017年专利授予件数占境内外专利申请件数的百分比是：

　　A. 47.4%

　　B. 49.6%

　　C. 50.3%

　　D. 56.6%

　　【答案】B

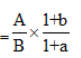
　　【解析】根据基期比重，选项出现了首位相同第二位不同的情况，先算一半，分母从左向右截取前三位，则基期比重<56.6%，发现选项A、B、C均<56.6%，排除不了，且选项较为接近，所以只能使用拆1法进一步确定正确答案。

　　拆1法公式为，代入数据即，B项满足。

　　因此，选择B选项。

　　以上就是关于计算基期比重、基期倍数、基期平均数的计算方法，在遇到此类问题时，首先判断题型，然后将公式列出，先用算一半方法判断选项的大致范围，如不能直接选出正确答案，那就需要采用第二种方法拆1法进一步确定计算结果。