400-633-0111
点击刷新
2023行测备考：赋值法和方程法在工程问题中的应用
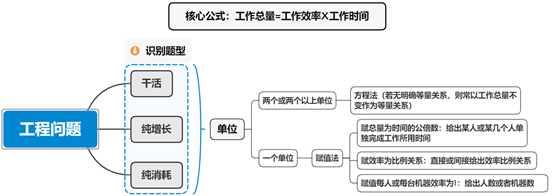
众所周知，在工程问题解题中常用的方法有赋值法和方程法，一般来说方程法和赋值法都是分别应用，我们对于方程法和赋值法的区分如下：当题中给出工作总量、工作时间、工作效率三类量中的两类或三类具体值，使用方程法;反之，一般只给出工作时间这一类具体值，则使用赋值法。
但是，结合近几年公务员考试的真题来看，单纯使用赋值法或方程法，不能帮助我们解决所有的工程问题，很多时候需要将赋值法和方程法结合起来。那么接下来我们通过一些例题，来探究如何将两种方法结合在一起解决工程问题。
【例1】现有一批零件，甲师傅单独加工需要4小时，乙师傅单独加工需要6小时。两人一起加工这批零件的50%需要( )小时。
A.0.6
B.1
C.1.2
D.1.5
【答案】C
【解析】赋值工作总量题干中只有工作时间这一类具体值，故使用赋值法。赋值工作总量为时间的公倍数24(4和6的公倍数)，则甲、乙两人的工作效率分别为6与4。题中问加工这批零件的50%需要多少小时?即加工零件24×50%=12。两人合作时，效率为6+4=10，根据工作总量=工作效率×工作时间，设需要时间为t，则12=10×t，解得t=1.2小时。
【总结】在解决本题时，最后一步很多考生在计算时通过工作总量=工作效率×工作时间，则工作时间=工作总量/工作效率，直接代入数据可得工作时间为小时。然则通过我们刚才解析所列，最后一步其实用到了方程的一个思想，故而我们在解决工程问题时，已经是将方程法和赋值法同时应用。
【例2】某商铺甲乙两组员工利用包装礼品的边角料制作一批花朵装饰门店。甲组单独制作需要10小时，乙组单独制作需要15小时，现两组一起做，期间乙组休息了1小时40分，完成时甲组比乙组多做300朵。问这批花有多少朵?
A.600
B.900
C.1350
D.1500
【答案】B
【解析】题干中给出甲乙分别单独制作完成所需时间，我们可以赋值工作总量为10和15的公倍数30，此时甲组与乙组的效率分别为3和2。由于题干最终的要求需要我们求出具体这批花朵的数量，故我们赋值的工作总量30仅为30份，需要求解一份具体为多少朵花，我们可以设每份花朵为x，即工作总量为30x，甲组与乙组的效率分别为3x和2x。
实际工作时，乙组休息了1小时40分钟即53小时，这53小时只有甲组在工作，其余时间为两组合作。甲组工作5/3小时，工作量为3x×5/3=5x，剩余30x-5x=25x的工作量为甲乙两组合作，所需时间为25x÷(2x+3x)=5小时，即乙组工作时间为5小时，甲组工作时间为5+53=203小时，根据“完成时甲组比乙组多做 300 朵”，可得甲组工作量-乙组工作量=300朵，即3x×203-2x×5=300，解得x=30(朵)，这批花一共有30x=30×30=900朵。因此，选择B选项。
【总结】在本题中，出现工作时间和工作总量这两类具体值，很多考生的第一反应应该用方程法解题，但是实际我们实际赋值了工作总量为30份，设每一份为x，最终令工作总量为30x,也将方程法和赋值法结合了起来。
综上所述，原先方程法和赋值法在工程问题中应用的区别主要看单位的个数，工程问题中共有3类量，如果有两类及以上的量带有具体单位，那么我们用方程法，反之则应用赋值法。通过上述两道题目的解析，我们可以看出，在解决工程问题时，只要题目满足可应用赋值法的某些条件(比如说，题干中给出某些主体单独完成工作所用时间;给出各个主体的效率比例关系)，我们便可以赋值总量或者效率，此时所赋值的总量或者效率单位即为份数，如果题干中给出的总量或者效率带有具体单位，则此时应将每份设为x，这就是将赋值和方程结合在一起的应用，各位备考考生可以自行去寻找相关的题目进行练习。
京公网安备1101082038637号