事业单位职业能力倾向测验资料分析中,平均数相关考点考生掌握薄弱,且在考试中正确率较低。掌握核心知识点及技巧,分数便可提高。基期平均数是平均数相关的重要考点,接下来,我们一起来学习基期平均数的答题技巧。
基期平均数是在基期的角度对数据进行平均数的考查,题型的特征往往是问题的时间与材料不一致,出现每、平均等字眼。一般基期平均数可以通过两种方式进行计算:
①已知现期量与增长量:基期量=现期量-增长量,基期平均数
②已知现期量与增长率:A为现期量总数,a为A的增长率,B为现期量总个数,b为B的增长率,基期量总数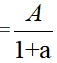 ,基期量总个数
,基期量总个数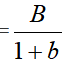 我们可以得出基期平均数
我们可以得出基期平均数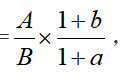 这是求基期平均数的常用公式。
这是求基期平均数的常用公式。
同学们以后在使用该公式计算基期平均数时,要记住一下四个字“算左看右”。“算左”即算该公式中的左半部分“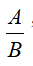 ”,“看右”即看
”,“看右”即看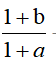 与“1”的大小比较,最终结合选项选出正确答案即可。
与“1”的大小比较,最终结合选项选出正确答案即可。
【经典例题】
【例题1】2017年全国共有各级各类民办学校17.76万所,占全国学校总数34.57%;各类民办教育在校生达5120.47万人,比上年增长6.12%。其中:民办幼儿园16.04万所,比上年增长4.00%;在园儿童2572.34万人,比上年增长5.53%。民办普通小学6107所,比上年增长2.21%;在校生814.17万人,比上年增长7.65%。民办初中5277所,比上年增长3.78%;在校生577.68万人,比上年增长8.42%。民办普通高中3002所,比上年增长7.71%;在校生306.26万人,比上年增长9.74%。民办中等职业学校2069所,比上年下降2.17%;在校生197.33万人,比上年增长7.16%。
2016年平均每所民办中等职业学校在校生人数约为:
A.871人 B.991人
C.1091人 D.1181人
【答案】A
【解析】第一步,本题考查基期平均数计算。
第二步,定位文字材料,“民办中等职业学校2069所,比上年下降2.17%;在校生197.33万人,比上年增长7.16%”。
第三步,根据基期平均数公式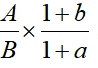 ,选项未出现首位相同量级不同的情况,无需换算单位,复杂计算,可将部分数据截位处理,代入数据可得,
,选项未出现首位相同量级不同的情况,无需换算单位,复杂计算,可将部分数据截位处理,代入数据可得,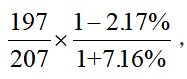 左半部分直除首两位为95,实际应为950多人,右半部分是一个小于1的数,故乘积必然小于950人。
左半部分直除首两位为95,实际应为950多人,右半部分是一个小于1的数,故乘积必然小于950人。
因此,选择A选项。
【例题2】2017年,我国技术市场交易额稳步增长,全年共签订各类技术合同36.8万项,成交金额13424.2亿元,比上年分别增长14.7%和17.7%。
2016年,平均每项技术合同成交金额约为:
A.330万元 B.356万元
C.365万元 D.385万元
【答案】B
【解析】第一步,本题考查基期平均数计算。
第二步,定位文字材料可知,“2017年,我国技术市场交易额稳步增长,全年共签订各类技术合同36.8万项,成交金额13424.2亿元,比上年分别增长14.7%和17.7%”,定位柱状图材料可知,“2016年,我国签订的技术合同成交金额为11407亿元”。
第三步,根据基期量 、平均数=
、平均数=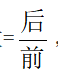 ,选项出现了首位相同,第二位不同的情况可将分母从左到右截取前三位,分母取整处理,代入可得
,选项出现了首位相同,第二位不同的情况可将分母从左到右截取前三位,分母取整处理,代入可得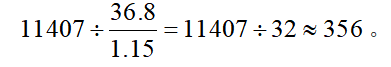 。
。
因此,选择B选项。
【例题3】2021年1-5月,全国共破获电信网络诈骗案件11.4万起,打掉犯罪团伙1.4万个,抓获犯罪嫌疑人15.4万名,同比分别上升60.4%、80.6%和146.5%。2021年5月,全国共立电信网络诈骗案件8.46万起,与4月相比下降14.3%。
2020年1-5月,全国平均每月打掉电信网络诈骗犯罪团伙:
A.不到1000个 B.1000~2000个之间
C.2000~4000个之间 D.4000个以上
【答案】B
【解析】第一步,本题考查基期平均数计算。
第二步,定位文字材料,“2021年1—5月,全国共破获电信网络诈骗案件11.4万起,打掉犯罪团伙1.4万个,抓获犯罪嫌疑人15.4万名,同比分别上升60.4%、80.6%和146.5%”。
第三步,根据基期量 ,平均数
,平均数 ,选项为范围,将分母从左向右截取前三位计算,代入可得2020年1—5月,全国平均每月打掉电信网络诈骗犯罪团伙约
,选项为范围,将分母从左向右截取前三位计算,代入可得2020年1—5月,全国平均每月打掉电信网络诈骗犯罪团伙约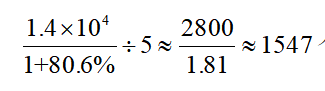 个,在B选项范围内。
个,在B选项范围内。
因此,选择B选项。
基期平均数是在基期的角度对数据进行平均数的考查,题型的特征往往是问题的时间与材料不一致,出现每、平均等字眼。一般基期平均数可以通过两种方式进行计算:
①已知现期量与增长量:基期量=现期量-增长量,基期平均数

②已知现期量与增长率:A为现期量总数,a为A的增长率,B为现期量总个数,b为B的增长率,基期量总数
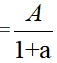 ,基期量总个数
,基期量总个数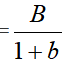 我们可以得出基期平均数
我们可以得出基期平均数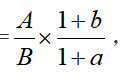 这是求基期平均数的常用公式。
这是求基期平均数的常用公式。同学们以后在使用该公式计算基期平均数时,要记住一下四个字“算左看右”。“算左”即算该公式中的左半部分“
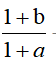 与“1”的大小比较,最终结合选项选出正确答案即可。
与“1”的大小比较,最终结合选项选出正确答案即可。【经典例题】
【例题1】2017年全国共有各级各类民办学校17.76万所,占全国学校总数34.57%;各类民办教育在校生达5120.47万人,比上年增长6.12%。其中:民办幼儿园16.04万所,比上年增长4.00%;在园儿童2572.34万人,比上年增长5.53%。民办普通小学6107所,比上年增长2.21%;在校生814.17万人,比上年增长7.65%。民办初中5277所,比上年增长3.78%;在校生577.68万人,比上年增长8.42%。民办普通高中3002所,比上年增长7.71%;在校生306.26万人,比上年增长9.74%。民办中等职业学校2069所,比上年下降2.17%;在校生197.33万人,比上年增长7.16%。
2016年平均每所民办中等职业学校在校生人数约为:
A.871人 B.991人
C.1091人 D.1181人
【答案】A
【解析】第一步,本题考查基期平均数计算。
第二步,定位文字材料,“民办中等职业学校2069所,比上年下降2.17%;在校生197.33万人,比上年增长7.16%”。
第三步,根据基期平均数公式
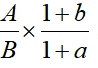 ,选项未出现首位相同量级不同的情况,无需换算单位,复杂计算,可将部分数据截位处理,代入数据可得,
,选项未出现首位相同量级不同的情况,无需换算单位,复杂计算,可将部分数据截位处理,代入数据可得,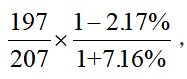 左半部分直除首两位为95,实际应为950多人,右半部分是一个小于1的数,故乘积必然小于950人。
左半部分直除首两位为95,实际应为950多人,右半部分是一个小于1的数,故乘积必然小于950人。因此,选择A选项。
【例题2】2017年,我国技术市场交易额稳步增长,全年共签订各类技术合同36.8万项,成交金额13424.2亿元,比上年分别增长14.7%和17.7%。
2016年,平均每项技术合同成交金额约为:
A.330万元 B.356万元
C.365万元 D.385万元
【答案】B
【解析】第一步,本题考查基期平均数计算。
第二步,定位文字材料可知,“2017年,我国技术市场交易额稳步增长,全年共签订各类技术合同36.8万项,成交金额13424.2亿元,比上年分别增长14.7%和17.7%”,定位柱状图材料可知,“2016年,我国签订的技术合同成交金额为11407亿元”。
第三步,根据基期量
 、平均数=
、平均数=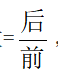 ,选项出现了首位相同,第二位不同的情况可将分母从左到右截取前三位,分母取整处理,代入可得
,选项出现了首位相同,第二位不同的情况可将分母从左到右截取前三位,分母取整处理,代入可得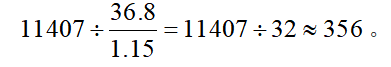 。
。因此,选择B选项。
【例题3】2021年1-5月,全国共破获电信网络诈骗案件11.4万起,打掉犯罪团伙1.4万个,抓获犯罪嫌疑人15.4万名,同比分别上升60.4%、80.6%和146.5%。2021年5月,全国共立电信网络诈骗案件8.46万起,与4月相比下降14.3%。
2020年1-5月,全国平均每月打掉电信网络诈骗犯罪团伙:
A.不到1000个 B.1000~2000个之间
C.2000~4000个之间 D.4000个以上
【答案】B
【解析】第一步,本题考查基期平均数计算。
第二步,定位文字材料,“2021年1—5月,全国共破获电信网络诈骗案件11.4万起,打掉犯罪团伙1.4万个,抓获犯罪嫌疑人15.4万名,同比分别上升60.4%、80.6%和146.5%”。
第三步,根据基期量
 ,平均数
,平均数 ,选项为范围,将分母从左向右截取前三位计算,代入可得2020年1—5月,全国平均每月打掉电信网络诈骗犯罪团伙约
,选项为范围,将分母从左向右截取前三位计算,代入可得2020年1—5月,全国平均每月打掉电信网络诈骗犯罪团伙约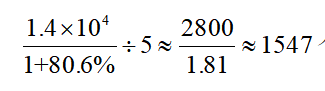 个,在B选项范围内。
个,在B选项范围内。因此,选择B选项。













 点击刷新
点击刷新













