数量关系

　　数量关系出题比较灵活，有的题目套路明显，但有的却不按套路出牌，我们一起来看一下。

　　(考生回忆)【例1】某品牌圆形扫地机器人升级设计方案，是在原有扫地机器人的前端伸出8cm可转运的边刷进行清扫(如下图所示，图略)，目的是将无法触及的边边角角都彻底清扫干净，那么，为了保证这一效果，该型号扫地机器人圆形机身的最大直径为：(答案取整数位)

　　A.30cm

　　B.36cm

　　C.38cm

　　D.40cm

　　试题分析：刚拿到这个题目，有的小伙伴不能准确的想出，如何才能找到扫地机器人最大的直径，无法构造出相应的几何图像，是一道不按套路出牌的题目，其实如果能构造出下图的图像，此题就迎刃而解;边刷长度为8厘米，只要边刷可清扫到顶角即可;利用勾股定理求解。

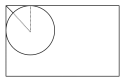
　　【解析】第一步，本题考查几何问题。第二步，边刷长度为8厘米，只要边刷可清扫到顶角即可。最大半径如图所示：设机器人圆形机身的最大半径为r厘米，可列方程：√2r=r+8，解得r≈19.3，那么最大直径为19×2=38(厘米)。因此，选择C选项。

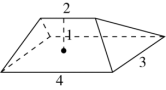
　　(考生回忆)【例2】下图所示是一种帐篷屋顶的示意图，底面是一个长4米宽3米的长方形，屋顶高1米，上棱长2米且平行于底面，那么该帐篷屋顶的体积是

　　A.5立方米

　　B.11立方米

　　C.12立方米

　　D.24立方米

　　试题分析：遇到这个题目，有的小伙伴看的有点懵，没有见过这类的立体图，不知道体积应该怎么求，是一道十分奇葩的题目。遇到这种题型，我们需要把它转化为规则图形的体积。即过上棱长两个端点向下垂直做两个切面，两侧是两个四棱锥，中间是一个三棱柱，则该帐篷屋顶的体积是两个四棱锥+一个三棱柱，然后分别求三棱柱、两个四棱锥的体积即可。

　　三、资料分析

　　下面我们盘点一下资料分析中不按套路出题的题目。

　　(考生回忆)【例1】2021年7月份，全社会用电量中第三产业用电量的占比比城乡居民生活用电量的占比相较约：

　　A.高3.3%

　　B.低3.8%

　　C.高9.8%

　　D.低10.3%

　　试题分析：材料中分别给出了2022年1-7月和7月的数据，考生需注意选择2022年7月数据，这是易错点。其次，一般题目只需要计算基期比重，但是这道题目需要分别求出基期比重，然后再做差。这题计算量较大，是不按套路出牌的题。

　　【解析】第一步，本题考查基期比重计算。第二步，定位文字材料第二段，“2022年7月份，全社会用电量8324亿千瓦时，同比增长6.3%;第三产业用电量1591亿千瓦时，同比增长11.5%;城乡居民生活用电量1480亿千瓦时，同比增长26.8%”。第三步，根据基期量=，和分数的性质，可得现期量大且增长率小则基期量大，第三产业用电量现期量(1591亿千瓦时)>城乡居民生活用电量(1480亿千瓦时)且第三产业用电量同比增长率(11.5%)<城乡居民生活用电量同比增长率(26.8%)，所以2021年7月第三产业用电量>城乡居民生活用电量，排除B、D选项。选项A、C首位不同，但是鉴于此题计算步骤较多，所以分母截取前三位代入数据，可得，首位商3。因此，选择A选项。

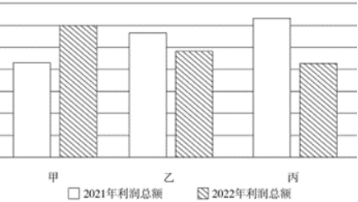
　　(考生回忆)【例2】下面柱状图中，甲、乙、丙依次代表

　　A.电气机械和器械制造业、非金属矿物制品业、医药制造业

　　B.化学原料和化学制品制造业、电气机械和器材制造业、汽车制造业

　　C.汽车制造业、电气机械和器材制造业、化学原料和化学制品制造业

　　D.医药制造业、非金属制品业、电气机械和器械制造业

　　试题分析：这道题考查了现期量比较及基期量比较，基期量比较类题目在柱状图中的考查比较新颖，一般考查形式中，让求最大、最小或排序较多，选项一般为主语或排序类，此题是不按套路出牌题目。此题可以先比较现期量的大小进行排除，再根据每个主体的现期量和基期量的大小关系判断增长率的正负，找数据进行排除。

　　【解析】第一步，本题考查简单比较中的读数比较。第二步，定位文字材料第三段全段。第三步，本题采用代入排除法解题。A选项：“电气机械和器材制造业”，利润总额增长31.2%，“非金属矿物制造业”，利润总额下降15.5%，“医药制造业”利润总额下降31.8%，依次对比甲乙丙图，基本吻合，因此A正确。B选项第一个是“化学原料和化学制品制造业”，其利润总额下降8.7%，显然与甲矛盾，因此排除。C选项第一个是“汽车制造业”，其利润总额增长0.6%，但甲图显示的增长率远远大于0.6%，显然错误，因此排除。D选项第一个是“医药制造业”，其利润总额下降31.8%，显然与甲矛盾，因此排除。因此，选择A选项。